The Basics
Roman numerals are written using seven different letters: I, V, X, L, C, D and M, they represent the numbers 1, 5, 10, 50, 100, 500 and 1,000.
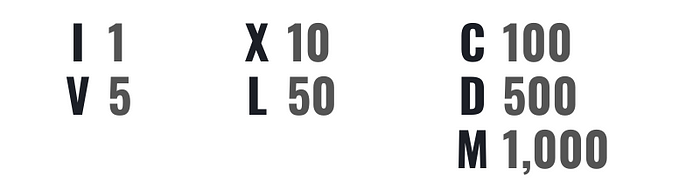
We use these seven letters to make up thousands of others. For example, the Roman numeral for two is written as ‘II’ which is just two one’s smushed together. The number twelve is XII which is just X (10) + II (2). If we take this a step further, the number twenty-seven is written as XXVII, which when broken down looks like XX (20) + V (5) + II (2) — all totalled up it equals to twenty-seven.
Similar reference: https://whatnumberisiv.com/
Roman numerals are usually written largest to smallest from left to right. However, this is not always true. The Romans didn’t like writing four of the same numerals in a row, so they developed a system of subtraction.
The Roman numeral for three is written III, but four is not IIII. Instead the subtractive principle is used. The number four is written as ‘IV’. Here we have I (1) before V (5) and because the smaller number is before the larger number, we know that we have to subtract here — making IV four. The same principle applies to the number nine, which is written as IX.
Related Articles:
What Number is VI? VI Roman Numerals Complete Information
There are six instances where subtraction is used:
- I can be placed before V (5) and X (10) to make 4 and 9.
- X can be placed before L (50) and C (100) to make 40 and 90.
- C can be placed before D (500) and M (1000) to make 400 and 900.
The number 994 is a great example of this rule — it’s written CMXCIV. Broken down we have CM = 900, XC = 90 and IV = 4; adding all these up brings us back to 994.
Read More : Wikipedia
Years and Dates
Years written in Roman numerals can be quite long and scary — but breaking them down we see that they’re actually quite simple. Let’s look at a few examples.
Years in the 21st century are nice ‘n easy. First, we start off with MM (1000 + 1000) and then we add on whatever we need. If we wanted to write 2020 in numerals we start with MM and add XX (20) to make MMXX.
Years from the 20th century are also quite simple. We start off with MCM (1900) and then similarly add on whatever we need. For example, 1985 would be written as MCM (1900) + LXXX (80) + V (5), which when written out is MCMLXV.
Here are the years in numerals from 2010 to 2029:
2010MMX2020MMXX2011MMXI2021MMXXI2012MMXII2022MMXXII2013MMXIII2023MMXXIII2014MMXIV2024MMXXIV2015MMXV2025MMXXV2016MMXVI2026MMXXVI2017MMXVII2027MMXXVII2018MMXVIII2028MMXXVIII2019MMXIX2029MMXXIX
Large Numbers
Because the largest letter used in Roman numerals is M and we can only stack three of the same numeral together the largest number you can write using standard numerals is 3999 (MMMCMXCIX).
But it is possible to write numerals bigger than 3999. If we draw a line across the top of a numeral then we are multiplying it by 1000.
For example, the Roman numeral for 5000 is written as V̅ (5 x 1000). Similarly, one million is written as M̅ (1000 x 1000).
If we want to write 1,550,000 in Roman numerals it would be written as: M̅ D̅ L̅. If we break it down the numeral for 1,000,000 is M̅, the numeral for 500,000 is D̅ and the numeral for 50,000 is L̅.

Zeros and Fractions
Interestingly there is no numeral for zero. This is because numerals were developed for the purposes of trading and there was no need for zero, instead the Latin word ‘nulla’ was used.
Fractions were often used in currency. The most common fractions used were twelfths and halves. A twelfth was represented by a single dot ‘•’, known as a ‘uncia’. Halves were represented by the letter ‘S’, short for semis.
Adding and Subtracting
With no numeral for zero, it makes doing any advanced mathematics a tad bit difficult — but addition and subtraction are well within the realms of possibilities.
ADDITION
When adding with numerals, the number one tip is to ignore the subtractive principle — i.e. instead of writing four as IV write it out as IIII.
Let’s take a simple example. To add IX (9) and XI (11) together, we:
- Convert IX to VIIII
- Arrange numerals from largest to smallest, giving us XVIIIII
- Simplify the IIIII to V, giving us XVV
- Simplify VV to X, giving us XX
SUBTRACTION
When subtracting numerals, we also ignore the subtractive principle. Let’s take the almost scary problem of CCLXXXVIII (288) — CCLXXI (271):
- First cross out all of the pairs of numerals (as seen below)
- Re-arrange the numerals and re-apply the subtractive principle where required
- Leaving us with our answer of XVII (17)

Modern Usage
Roman numerals can be found all everywhere in modern society, here are five examples:
- Roman numerals are used to refer to kings, queens, emperors and popes. For example; Henry VIII of England and Louis XVI of France.
- Many competitions such as the Super Bowl and Olympic Games use numerals to represent how many times the event has been held. For example, in 2021 it will be Super Bowl LV.
- Numerals can often be found on buildings and monuments to signify the year of construction. For example, a building built in 2004 may have the numerals MMIV engraved on it.
- Many movies use numerals to say when the film was made. For example, ‘Gladiator’ was copyrighted in the year 2000 and has the numerals MM at the end of its credits. Another example is the film ‘Spartacus’ which has MCMLX (1960) at the end of its credits.
- Many clocks also use numerals to represent the hours.
The list goes on and on, numerals can be found in books to number the introductory pages, in legal contracts to denote sections and sub-sections, to reference wars (WWI and WWII), et cetera, et cetera…
Origin of Roman Numerals
Before the Romans other civilisations had devised their own counting systems. The Etruscans who occupied central Italy before the Romans had developed a similar system which just used different symbols.
THEORY 1
A common theory is that the numerals represent hand signals. The numbers one, two, three and four are signalled by the equivalent number of fingers. Five is represented by separating the thumb and fingers to make a ‘V’ shape. The numbers six to nine are shown by one hand gesturing five and the other with the appropriate number of fingers. Ten is shown by crossing either hands or thumbs in an ‘X’ shape.
THEORY 2
Another theory suggests numerals originated from the notches etched onto tally sticks. These tally sticks had been used centuries prior to the Romans for basic counting; in fact, they were still used by shepherds in Europe until the 19th century.
The numbers one, two, three and four were represented by the equivalent amount of straight lines etched into the wood. Five was shown as an upside down ‘V’ and ten by an ‘X’.
This system followed similar principles to numerals. Seven on a tally stick would look like: IIIIVII, which would be shortened to VII. Taking another example, seventeen in long form would look like IIIIVIIIIXIIIIVII, but in short form: XVII.
The theory suggests that the Romans developed this system adding ‘L’, ‘C’, ‘D’ and ‘M’ to represent 50, 100, 500 and 1000.
Other Number & Counting Systems
Many other civilisations in the ancient world had already come up with their own number systems and methods of counting. We’re going to take a quick look at the Egyptian and Babylonian counting systems.
EGYPTIAN NUMBERS: 3000–1600 BCE
One of the oldest number systems comes from Egypt — developed over 5000 years ago! Their system was very comprehensive compared to others; they even had a symbol to represent infinity! Unlike the Romans, the Egyptians did have a symbol for zero.
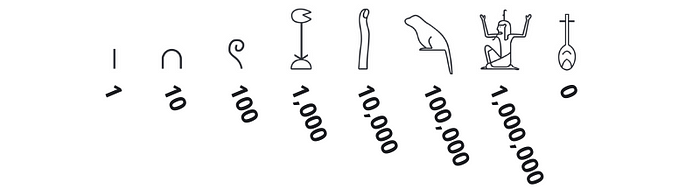
The Egyptians didn’t use the subtractive principle and with no symbol for five it meant nine was shown as nine I’s written out. To take another example 1700 was written as:

BABYLONIAN NUMBERS: 1750 BCE
The Babylonian system of numbers was also quite complicated; they actually adopted and adapted their system from the earlier Sumerians. Similar to the Egyptians, there was no symbol for five, meaning nine was also written out as nine 1’s (see the chart below). One thing the Babylonian system had in common with the Romans’ was having no symbol to represent zero.
